Objective Analysis
of
Time Stretching Algorithms
Abstract
This research describes and implements new techniques for objective analysis and comparison of common time stretching algorithms. A set of test signals and samples is used in conjunction with spectral analysis to generate objective error measurements and subsequent comparisions of the algorithms. The time stretching techniques are treated as black-box processes, and are regarded as members within a general family of analyze-modify-resynthesize algorithms. This black-box approach of output signal analysis provides a basis for objective evaluation of the more general class of algorithms. Six common time stretching algorithms are analyzed: the classic phase vocoder, oscillator bank phase vocoder, peak tracking phase vocoder, phase-locked vocoder, synchronous overlap add technique, and overlap add technique. The six algorithms are then compared within a uniform framework to provide greater insight regarding the behavior of their output signals. Subjective listening evaluations are also performed, then all results contribute to the development of criteria that evaluate and rank the algorithms’ suitability in various signal processing situations.
Download
Objective Analysis of Time Stretching Algorithms.pdfResources
| • Audio | – browse audio files |
| • Audio.zip | – download audio files |
| • Graphs | – browse graphs |
| • Graphs.zip | – download graphs |
| • Scripts | – browse scripts |
| • Scripts.zip | – download scripts |
| • All.zip | – download all resources |
Citations
| M.L.A. | — | Baker, Cooper Everett. Objective Analysis of Time Stretching Algorithms.
Diss. University of California, San Diego, 2015. |
| A.P.A. | — | Baker, C. E. (2015). Objective Analysis of Time Stretching Algorithms
(Doctoral dissertation, University of California, San Diego). |
| Chicago | — | Baker, Cooper Everett. Objective Analysis of Time Stretching Algorithms.
Diss. University of California, San Diego, 2015. |
| ProQuest | — | http://gradworks.umi.com/37/04/3704219.html |
Analysis Example
In total, this research uses six test signals in conjunction with three analysis techniques to evaluate six time stretching algorithms. The techniques and algorithms are described in detail, and 128 different graphs representing the resultant data are interpreted and comparatively discussed. This particular example was selected to briefly illustrate a facet of the research and provide a general idea of what the work is about.
1 — Test Signal
Analysis of the Phase-Locked Vocoder in this example is performed using one of the special test signals shown below. This test signal is designed to be difficult to stretch, and consists of a steady 1000 Hertz sinusoid mixed with a logarithmically swept sinusoid that moves from 50 to 21,000 Hertz.
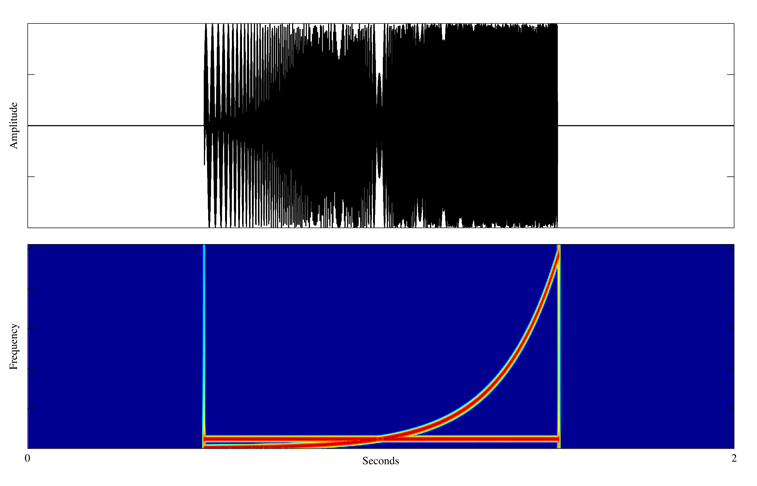
The input signal is synthesized with a duration of two seconds and an another ideal output signal is synthesized with a duration of four seconds. This allows comparison of the ideal output signal with the stretched output signal when the Phase-Locked Vocoder is configured to stretch its input by two times. The input, ideal, and stretched signals used in this example may be heard below.
2 — Phase-Locked Vocoder
Time stretching of the input signal is performed by the Phase-Locked Vocoder developed by Miller Puckette. This algorithm is similar to the Classic Phase Vocoder, however, it produces higher fidilety results by mitigating phase errors with a technique that locks phases of adjacent bins together before resynthesis. The following formulas show its operation, starting with a Discrete Fourier Transform (DFT) that generates spectral data where X contains the spectra, w is the window function, x is the signal, H is the hop size in samples, S is the stretch factor, N is the window size in samples, and F is the number of frames:
Phase accumulation occurs next, where P contains accumulated phase, over-bar signifies the complex conjugate, and Y[f-1,k] represents the previous output spectrum:
Following phase accumulation, phases are locked together into L, with the notation k-1 and k+1 signifying bin offsets, so that phases of three adjacent bins are combined:
After adjacent phases are combined, the output spectra are calculated as Y:
Finally, the output signal is windowed and overlap-added into y:
3 — Moving Spectral Analysis
Moving Spectral Analysis was developed for this research to provide information about the behavior of a stretched signal over time. This technique affords insight about time domain features like transients or persistent amplitude modulations by comparing them to their counterparts in the ideal signal. In order to create meaningful comparisons, the signals are power-normalized according to the following equations, where x is the audio file, w is the windowing function, A is the start of the signal region, B is the end of the signal region, and R is the Root Mean Square (RMS) power value:
R is then used to perform power-normalization of the stretched file so that it matches the ideal file as shown by the following equation, where xs is the stretched file, Rs is the stretched RMS power value, Ri is the ideal RMS power value, xsr is the power-normalized stretched file, and N is the length of the file in samples:
Following normalization, Fourier analysis is used to compare the signals’ spectra, frame by frame, to create a measure of difference between the ideal and stretched versions. The first step is implemented with a DFT where X represents the output spectrum, N is the number of samples per analysis frame, w is the window function, x is the signal, H is the hop size in samples, and F is the total number of frames:
The next step is the calculation of a set of moving average magnitude values over time, or magnitude curve, according to the following equation, where M contains the magnitude curve:
The windowing function is then normalized out of the magnitude curve, and the magnitude curve is converted to sones as represented by S, shown here by the following equation:
After creating the sones curves in S, the following equation uses these curves to calculate an error curve that shows how the two signals differ. E represents the error curve, Xi is the ideal spectrum, and Xs is the stretched spectrum:
Finally, the average and maximum error values are determined according to the following equations, where Eavg is the average value of the error spectrum, and Emax is the maximum value of the error spectrum:
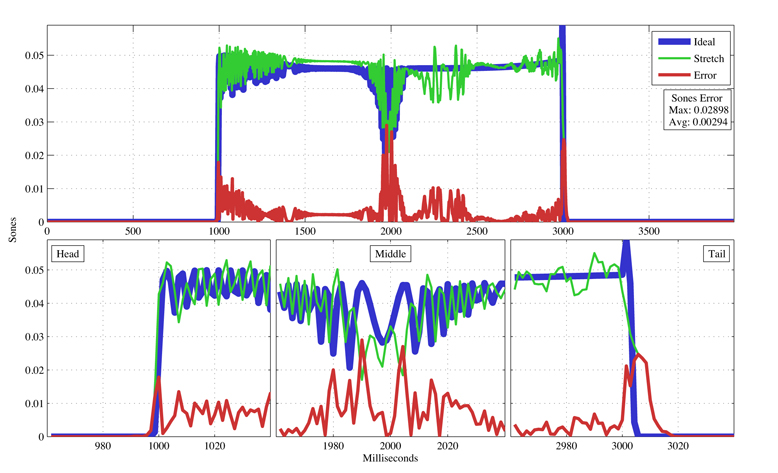
4 — Analysis Graphs
The following graphs show the ideal swept sinusoid signal in blue, the stretched version in green, and the error, or absolute difference, in red. Error is scaled in sones on the Y axis to more closely match our perception of sound, and the X axis displays the ideal and stretched signals over time, while also providing a more analytical representation of their differences than our ears can perceive. The upper graph is an overview of the entire signals, and the lower graphs show more detailed views of interesting areas within the signals.
